[고급 알고리즘] Graph(Shortest Path): Dijkstra Algorithm

1. Dijkstra Algorithm

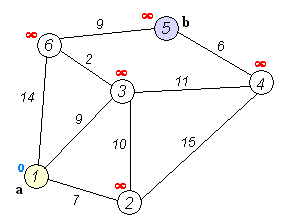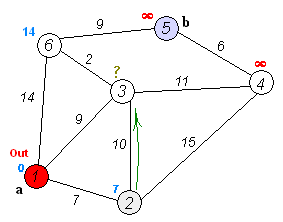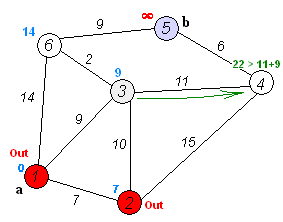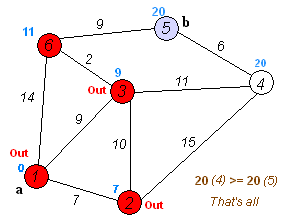
• 시작 정점으로부터 다른 모든 정점까지의 최단 경로를 찾는 알고리즘
• ✅ 음수 가중치가 없는 그래프 (양수 or 0)

 

Greedy

• 가장 짧은 거리를 가진 정점을 하나씩 확정해 나갑니다.
• ✅ 우선순위 큐와 인접 리스트를 사용하여 구현합니다.

 

2. 동작 원리

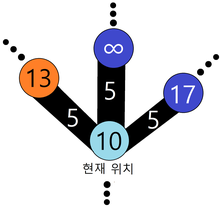
• 각 정점마다 출발지로부터의 최단 거리를 저장하며 탐색을 진행합니다.

 

초기화

• ✅ 출발지 거리 = 0 (자기 자신에서 출발하므로)
• ✅ 모든 교차점의 거리 = INF (현재 해당 교차로로 가는 최단 거리를 모름)

 

완화

• 현재 정점과 연결된 모든 이웃 정점에 대해 기존 거리보다 더 짧은 경로인지 확인합니다.
• ➡️ 기존 거리보다 더 짧은 경로라면, 그 경로로 거리 값을 갱신합니다

 

반복

• 우선순위 큐가 비거나, 모든 최단 거리가 확정될 때까지 완화 과정을 반복합니다.
• ✅ 우선순위 큐에서 꺼낸 정점의 거리 값은 최단 거리로 확정됩니다.
• ➡️ 각 정점에 대한 최단 거리 정보는 계속해서 갱신됩니다.

 

3. 구현

static class Edge implements Comparable<Edge> {
    final int dest, weight;

    public Edge(int dest, int weight) {
        this.dest = dest;
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge o) {
        return Integer.compare(this.weight, o.weight);
    }
}

private static void dijkstra(int start) {
    Arrays.fill(minDist, Integer.MAX_VALUE);
    visitBit.clear();

    minDist[start] = 0;
    pq.offer(new Edge(start, 0));

    while (!pq.isEmpty()) {
        Edge curE = pq.poll();
        int stopover = curE.dest, toStopOverD = curE.weight;
        int minStopOverD = minDist[stopover];

        if (toStopOverD > minStopOverD) continue;
        if (visitBit.get(stopover)) continue;
        visitBit.set(stopover);

        for (Edge destE : edges.get(stopover)) {
           int dest = destE.dest, toDestD = destE.weight;
           int newD = minStopOverD + toDestD;
           if (newD >= minDist[dest]) continue;

           minDist[dest] = newD;
           pq.offer(new Edge(dest, newD));
        }
    }
}

Time Complexity: O(E log V)

 

출처

• Wiki - Dijkstra Algorithm